Ildar Khabibullin.
Ildar Khabibullin, Ph.D. in Physics and Mathematics, research scholar at high-energy astrophysics department of the Institute for Space Research of RAS and Astrophysics Institute of Max Planck Society (Germany), won this year Yakov Zeldovich medal for substantial contribution to decoding early high-energy activity of supermassive black hole Sgr A* in the center of our galaxy and insight into the nature of physical processes going on in galaxy collapsed stars. He told our portal about what makes black hole Sgr A* interesting, what people should study the processes taking place in our galaxy and other ones for, and why some observation of some space objects looks like watching a mouse.
- Ildar, this year you have won the Yakov Zeldovich medal. Tell me, please, about your research.
- To begin with, I would rather tell you about Yakov Zeldovich medal. The award was established by the Russian Academy of Sciences and international commission of the Committee on Space Research for space research with the help of mostly observatories. It is awarded every two years when the assembly of the Committee is held.
Yakov Zeldovich Medal.
In general, there is a large enough range of research segments that the scientists deal with. This data is directly related to space research carried out with the help of observatories launched from the Earth. The joint work that my colleagues and I performed and which served as the grounds for winning the medal, on the one hand, was devoted to studying the history of activity Sgr A*, a supermassive black hole in the center of our galaxy, with the help of reflected x-radiation, x-ray echo that we observe coming from molecular clouds in it vicinity. On the other hand, there were works related to studying black holes and compact objects lower in mass which form up as a result of advanced stage of the stars’ evolution. When the life of stars is over, they sometimes get transformed into black holes. WE have also dealt with investigating the processes that take place in the vicinity of such objects in certain conditions.
- Why was black hole Sgr A* chosen? Is it more interesting if compared to other ones, or is it different from other black holes with regard to processes taking place inside it?
- It is supermassive black hole Sgr A*. Sgr stands for Sagittarius (the Latin for archer). It is located in the constellation of Sagittarius and has number A with a star, i.e., it is the brightest object in the radio-frequency range of Sagittarius. Sgr A* is point-type object. As was discovered at that time, it had no extensive radiation detected with the help of telescopes. This black hole is one of the main objects in our galaxy. It is located in the very center of it and likely to have taken shape at an early stage, simultaneously with the moment when our galaxy was born. After that, they continued to evolve together somehow.Though its direct impact is limited to its locality alone, as the gravitation potential of galaxy, star and other components quickly start imposing greater influence on what happens there, but thanks to being a black hole, it is capable of releasing a large amount of energy within short periods of time. During the periods of excessive burst activity, it is capable of emission higher than all stars of our galaxy and releasing energy in substantially larger quantities. At such moments it can make an impact on everything that take place in our galaxy: the process of tars’ formation and pattern of gas distribution in the whole area, even the most distance outskirts of the galaxy. Due to such relation and ability to impose influence, the so-called feedback communication cycle is launched, i.e., the growth or activity periods of the black hole are closely interrelated with the life of galaxy in general. That is why this object is essentially important for both our galaxy and all other ones that we know about.
It is interesting that our supermassive black hole demonstrates very tranquil behavior in the current period. It radiates by about 10 billion times less energy than it could during the periods of becoming active. On the one hand, it provides opportunities for studying the details and nuances that would not be seen in the periods of excessive activity. On the other hand, it is always interesting to set a number of questions. When has it been active for the last time? How it all happens? How does the process begin? When does it start absorbing the substance, radiate energy and impose influence?
Center of Milky Way galaxy with black hole Sgr A*
Observing the galaxy in general, we see the traces of the fact that Sgr A* was probably active 20-30 million years ago. It was active in the sense of imposing influence on all what happened in the galaxy. It is also possible that from time to time some careless star passing by turns out to be torn to pieces by way of high tide. Like the Moon causes high tides on the Earth, a star may be turn to pieces in high-tide field of the black hole. Then parts of this matter – fragments, scraps of the star – are absorbed, while the black hole tarts radiating energy. It I a very short phenomenon a rule, it lasts about one of several years.
Besides, in general, as it often happens in high-energy astrophysics, energy processes take place all the time in the form of low-amplitude bursts which we observe on the Sun for instance.
We notice solar flares, and the same burst activity takes place in the vicinity of black hole. Even being in quiescent state it transforms into a different state from time to time and bursts. At such moments, the release of energy rises, well, not by 10 billion times, but by 100 or even 1,000 times. It is what we continuously observe on our supermassive black hole.
So what we have dealt with was about the following. We would like to come back to the scopes typical for the period of hundreds of years ago and look whether this supermassive black hole was brighter at that time. Well, I do not mean by 10 billion or 100 times brighter… We were interested in whether the black hole demonstrates the periods of intermediate activity. Astrophysics features a great advantage – looking far ahead we observe the past. It is because light needs time to travel from one point to another.
Thus, it appears that if we divide space distances by the velocity of light, i.e., the speed of its propagation, they turn out to be longer than the period of human life. It allows for studying the historical events live. Watching the molecular clouds located in the vicinity of the back hole, we can take a look into the past of this black hole, as it takes about several hundred years for the light to cover the distance from the black hole to this cloud and disperse in our direction, as we observe it only afterwards. Such x-ray echo that we observe allows, on the one hand, to study the molecular clouds as they are illuminated by the black hole and to explore the past activity of the black hole itself.
At some moment, we have developed an interesting mathematical tool which helps us to analyze the properties of this radiation, its variation across time, or variableness, as we call it, a well as its spatial properties. Knowing what they depend upon in physical condition in interstellar environment, one can come to certain suggestions with regard to the relation of their statistical features.Taking advantage of them, we could find out accurately enough that about 100-120 years ago our supermassive black hole had really been one million times brighter than today using the scale of about one year. As for the reason behind it, we do not know it for sure. There may be several variants. The star explosion which I have mentioned before does not fit, as it would have been even brighter event. However, this event featured lower radiation of energy. We know that our supermassive black hole was one million times brighter during the period of 1-1.5 years. It allows us to study its history a well.
In general, this supermassive black hole attracts special attention because it is closest object to us. It is located in our galaxy, and there are no such objects more in the galaxy. Only the neighboring one can boast of having such black holes. That is why we are able to study it even better. This year, the Nobel Prize was awarded right for exploration of this supermassive black hole with the help of cutting-edge observatories. After 15 years of continuous observation, the scientists could see how the orbits of individual tars located around this black hole change. As it has turned out, they change in full accordance with the relativity theory formulated by Einstein. The basic prognoses were verified, and it allowed for measuring the distance to this supermassive black hole, its mass and other parameters with exceptional accuracy. It means that it is the most rummaged supermassive black hole today in particular, and one of the most thoroughly studied space objects in general.
- How are the black hole studied? What data do the observatories collect? Can the black holes be studied with the help of terrestrial observatories, or space one are required?
- Many changes have taken place in this field recently. Initially, the observation component part of this process was being developed mainly with the help of x-ray space observatories. What should we launch x-ray observatories into space for? The reason behind it I about the very atmospheric column that, according to the shrewd remark by Ostap Bender (main character of novels by Ilf and Petrov), puts pressure on the communist party officials as well.
This atmospheric column protects us from x-ray radiation coming from space, as the atmosphere is not transparent for it due to the fact that there are atomic transitions on the respective wavelengths. That is why one has to leave the atmosphere, its dene part at least, to observe anything in x-ray range.
There are various methods to do it – to launch a rocket or rise into the sky on a balloon and reach the stratosphere. Or one can launch an observatory and put it into the earth orbit. The very first observations made by the scientists who had launched such observatories showed that there are a large enough number of bright x-ray radiation sources in the sky. About 60 years ago a hypothesis was put forward saying that that the source of radiation in these objects – the energy of black holes – is a substance that is caught by this gravitational potential, heats up to the temperature of about 10 million degrees minimum and starts emitting x-ray radiation. These temperature figures are similar to the ones that we have in the center of the Sun or solar corona, which also emits radiation in x-ray range. At that time, they were called candidates to black holes, yet nobody could say for sure that they were black holes indeed. Other candidates included very distant objects, the so-called quasars – the nuclei of distant galaxies which also release a huge amount of energy. It looks like the supermassive black hole in the center of our galaxy, yet a thousand times more powerful. Their radiation is very bright, and we can see it from the most distant areas of the universe.
In general, that is how the process of studying black holes was initiated. Further on, the individual objects of our galaxy were described better, and their mass was measured. It turned out that they may exceed the un by 10 times in mass. Using the typical prognoses in the theory of stellar evolution, we can say that such objects must be black holes.
Two fundamentally new methods of studying these objects have been developed recently. One of them I related to interferometer measurements, the observations in radiofrequency range. This method makes observations and measurements possible from Earth, for instance, from Atacama Desert in Chile. You have probably heard about the first image of black hole having been obtained. It was obtained just for such a supermassive black hole located in the nearest galaxy cluster, namely galaxy M87, constellation of Virgo. As it is a huge black hole, the size of it as seen in the sky is also large. Beside, this galaxy cluster is the closet one to us (our system is even a part of its zone of influence). That is why its size as seen in the sky is comparable to the one our supermassive black hole has. It means that the telescopes with parameters which are required and available in radiofrequency range now are applicable for both objects, and thee object can be studied. Yet, as the more distant black hole is one thousand times larger than our one, the processes in it are much slower, put it crudely. That is why observing it as an elephant we can get the full picture, which is better than chasing a mouse which is hard, even impossible to catch. Sooner or later, however, in the course of accumulating the required data, we are likely to obtain a similar picture for our galaxy.
Finally, the latest technological achievements are related to observation of gravitational wave events – the collision of black holes or neutron stars. It is a discovery of the past few years. The sensitivity of these new systems that measure gravitation field near us allows for identifying that at some moment (and we get a signal typical for this process) two black holes start lowly rotating relative to each other coming closer and closer to each other, quicker and quicker, and finally merge. It is this very characteristic, typical prognosis, which on the background of strong noise exiting there allows for finding such events.
At present, the number of such events I enough to start studying their population properties and compare them to the population of black hole that we observe in x-ray range in our galaxy. Thee gravitation wave events take place in distant galaxies. The advantage of gravitation wave observations lie, among other things, in the fact that they are much less sensitive to distance if compared to conventional observation of electromagnetic radiation, so one can comfortably observe them from a very far distance.
The first real image black hole’s shadow in galaxy Messier 87, constellation of Virgo.
- How are the images of these black holes obtained?
- Today, the most advanced astrophysics has turned into the work involving huge data arrays. A far as the aid image of supermassive black hole is concerned, the scientists decided that it would be quicker to carry the data from Chile to Europe by airplane than transfer it through the Internet, i.e., the data amount was so huge that that they recorded it on CDs and transferred by air. Later, they spent a lot of time to perform what we call cross-correlation of this raw data that is obtained directly from telescopes by way of comparing the information obtained at different places from different telescopes.
It is cross-correlation that results in obtaining the final product – the final picture. It contains certain information itself, yet one should understand here the scale of signal relative to the noise that is always present in it. It often happens that one can identify the image as being noisy just having looked at it, as there are random fluctuations. However, it is true only for statistical noise. If the noise is systematic, we can fundamentally fail to see it. In this case we would just smoothly distort the final picture. One image is not enough here as a rule. Besides, it is important to realize what kind of uncertainty of methods it features. It also takes a lot of time from the point of view of description and modelling. I.e., we have to model the whole process, from the very object, its initial model, to put it through the model of telescopes, through the model of data processing and compare the result with what is seen. The whole operation is performed several times in iterative way, and finally the result that everybody sees is obtained. Usually, the following process takes place: a large amount of raw data, the cross-verification of it, various ingle-blind tests and the final result. It is important to minimize the effect of obtaining information and data processing in the final result. It is a serious area of research from the point of view of processing astrophysical data. Various methods are suggested in order to avoid the so-called confirmation imbalance or distortion. If a dozen people have said before that a certain event happens in a certain way, it becomes disadvantageous to affirm that it is not so due to pure sociological reasons. People tend to confirm the previous results rather than deny them. That is why the scientists perform blind testing first, i.e., they randomly shift the parameters and do not know what kind of data they actually get. They open their eyes at the very last moment, make the right calibration settings and look at the result they get. Fundamentally, this I the way to avoid distortions.
Another method lies in several teams processing data independently of each other with the result being cross-checked at the end. It means that obtaining the final picture or result involves serious and hard work today. Sometimes, it requires the cooperation of many people and involves various problems associated with data processing and transfer, as well as psychology of research activities.
- You have mentioned before that the black hole which you study today is one of the highly-researched ones, as it I located in our galaxy. Is it more honorable to study distant galaxies, or it makes no difference which galaxy the scientist studies?
- It seems to me that word honorable is inappropriate here. On the one hand, it is the question of individual interests. On the other hand, it is about some people like pictures, while others like cinema. Our galaxy is like a picture in some sense. We look at it as at a static picture and can study it in detail. As for exploring other galaxies, it allows us to watch a movie. We watch the galaxies to evolve. As there are lots of them, we watch the whole population of them. We see young galaxies and older ones, as well as the galaxies having the same and different features. We see all this diversity, yet with lower degree of detailing. We detect individual important elements in evolution or certain properties. However, it I impossible to obtain such details that we can get studying our galaxy.
In general, there are galaxies which are very much different from our one due to various reasons. There are a lot of effects that we cannot observe directly in our galaxy, because they occur very seldom. For instance, such events as the destruction of star by a black hole take place approximately once in 30 thousand years. Taking into account how long the history of mankind is, we can hardly trace them. On the other hand, having observed millions of other galaxies, we will certainly find such events. They should just happen statistically, so the observation of such rare events is actually becoming the norm.
Thu we cannot and should not distinguish between the activities that are honorable or not. It I rather a question of individual liking. In general, astrophysics as a science is involved in social moments. It is related to such things as what ideas are prevailing today, and which area can boast of having better observation data.
The area where we can get new knowledge in becomes more interesting to some extent. As it turns out, the process of development goes almost in a parallel way. I mean that our galaxy is studied along with other ones. The fact is that people put into operation different observatories and obtain the data that I also widely different. As far as the exploration of our galaxy is concerned, observatory GAIA (Global Astrometric Interferometer for Astrophysics) presents a lot of information of remarkable quality. It deals with measuring and analyzing the positions of stars in our galaxy and their movements. It allows for feeling their dynamics, the way they are moving. On the other hand, the number of reviews from large systems in the sky is growing. Their data let us see distant galaxies and analyze their evolution. The launch of James Webb Space Telescope will become a very important step in this direction, as it will allow for studying the evolution of distant galaxies in detail. It is just what concerns galaxies alone, but there are very many individual objects that are of interest for exploration.
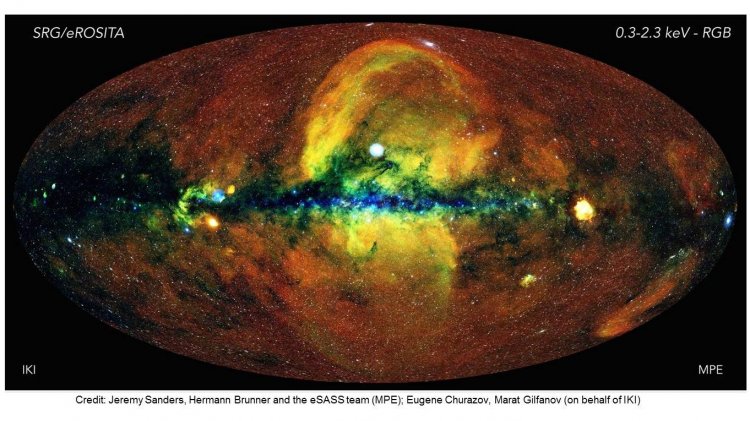
Celestial map obtained with the help of observatory SRG/eROSITA
Photo source: Institute for Space Research of RAS
- The stars are located far away from us. What should we study astrophysics for?
- This question was set to many of my colleagues, and many different answers were given. The answers are many, as astrophysics is a diverse science producing different results, and the people are different. If we take reasons instead of goals, it seems to me that people study astrophysics because they always need a bit more than they have. It is probably a very important driver of civilization.
Another moment lies in the fact that accumulation of knowledge takes place. The mankind I accumulating knowledge all the time, and each generation can boast of having the knowledge of previous ones. This phenomenon is even much more pronounced in the field of science. Browsing the Internet today, one can find articles written 150 years ago or the scholar papers created in the distant past. Gradual accumulation of knowledge leads to the fact that the things which are actually new are few in number. The question is where these new things can be found. Astrophysics in particular is a sort of window to a different world, which offers a hope for new knowledge to us. It is this need, or, to some extent, the hopelessness of the world around us from the point of view of new knowledge, that urge us to study a different world that offers hope for obtaining new knowledge. So far, this window has been working well. We can observe a lot of different new phenomena there, or the existing phenomena in a clearer way, as some process play more important role, while other ones are less important. It is the laboratory that allow for seeing the processes that go on in a different way.
Then, a question springs up as to how these phenomena are related to what we see around us. When people hear the perceptual tory about Newton discovering gravitation, the majority of them picture to themselves an apple falling from the tree. In general, the story is much more profound. Once there lived astronomer Tycho Brahe. He was so successful in developing astronomy that the king of Denmark gave to him as a gift an island and built the city of Uraniborg on it, the one for astronomical observations. It happened in Europe which suffered from the epidemic of plague at that time. The king’s motivation was naturally far from the passion for astronomy, but astrologically related. One way or another, Tycho Brahe could perform systematic observation of celestial objects for over 10 years and drew up a table of them.
Later, he handed over this table to Johannes Kepler who derived the laws of celestial motion (Kepler’s laws) using them. He found out that the planets are moving along elliptical orbits and formulated other laws linking their periods to orbit sizes. After that, Isaac Newton realized that the force that moves the planets and the one moving the apple is one and the same force. He established relation between the celestial objects and the ones that were around him. It is this step of relating something distant to something close allowed him to formulate the law of inverse squares and the thing that we know today as gravitation theory in general. It is one of the classic examples that show how studying the things which seem unrelated may finally lead to discovery of such fundamental laws as the one of gravitation.
We cannot say that it I a sort of banality, or that the English peasants started catching apples better because Newton discovered his law. Moreover, these laws became important for the mankind only hundreds of years later, when artificial satellites of Earth started being brought into orbit, and the world around us stopped being flat. In our everyday experience, we may consider the gravity field as a uniform one with constant free-fall acceleration. Only hundreds of years later, this discovery started playing an essential role. In general, such discoveries always start playing their roles some time later. It is due to our, probably unconscious, desire to explore new things – as we always want a bit more – that we study what we do not need. However, the things that we do not need today turn out to become necessary year later.
- Tell me, please, about your last research projects. Do you continue to deal with studies that brought the medal to you, or you deal with a new research project?
- We continue to study our supermassive black hole. We have filed an application for long-term observation which will allow for improving the previous data and obtain certain new information data dealing this time with the molecular clouds which are irradiated by the black hole. I.e., we expect to take a glimpse inside the clouds in the same way as we have got the x-ray image. Thanks to the x-ray burst produced by the black hole we are screening the inner structure of molecular clouds.
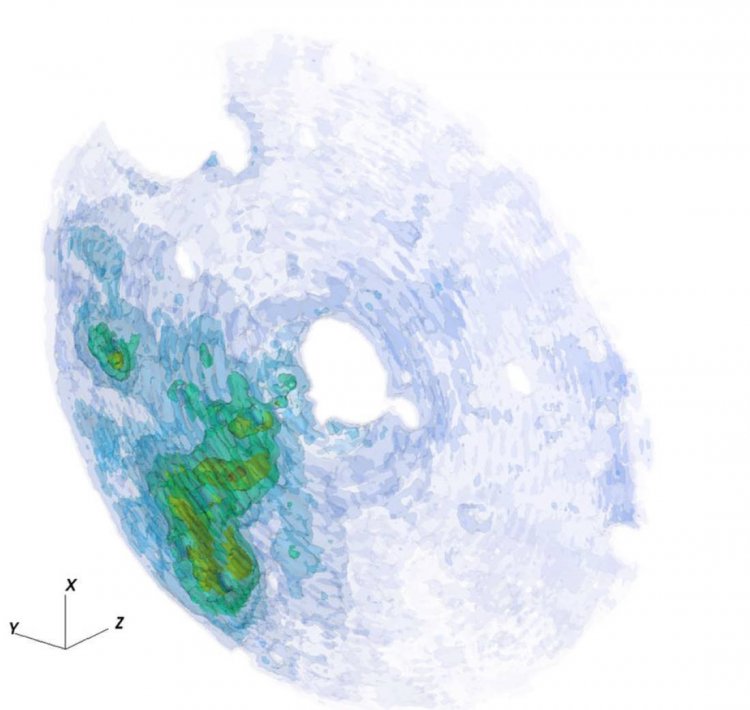
Three-dimensional distribution of dene interstellar gas in the vicinity of black hole SGR A* in the center of our galaxy restored with the help of x-ray echo of a short radiation burst. The burst occurred about 120 years ago.
Illustration: © Churazov, Khabibullin, Sunyaev, Ponti, 2017
can trace the structure of molecular clouds – from the largest one in the suburbs to the nuclei which give way to the birth of new stars. The paradigm of the current star formation is such that there are comas of relatively cold substance in which energy dissipation gradually takes place. They cannot resist to gravitation and start huddling together. Eventually, the tars form up in these very nuclei. Using the example of these clouds, or some specific cloud that has been irradiated, and taking advantage of this unique opportunity, as the black hole scans the cloud by x-ray methods, we wanted to look and see what happened inside it. Observations are to be taken this year, and we hope to get definite answers to our questions.
Besides, we will also take subsequent observations aimed at measuring not only intensity or spectrum of x-ray radiation, but polarization as well. In general, it is an additional window, and we all have been looking forward to it for a long time. The polarization of x-ray radiation – a very interesting parameter – has been measured so far only for one object. Among a great number of objects emitting x-ray radiation, only one was bright enough and could boast of sufficient polarization to measure the signal. We expect the launch of a new observatory with the mission aimed at this very area of research. In this case, we will get the results of new measurements and be able to study various new aspects.
At present, we devote a lot of time to the work with data provided by observatory Spektr-RG and specific device installed on it – eROSITA – which are dealing with celestial observations today. At the initial stage, when the observatory was just starting its research activities, it could take a series of explorative observations, which were selected so that they allowed for verifying the device characteristics and obtain a new area of research. The device characteristics turned out to be such as we had expected, while the goals and objectives that we had set proved to be attainable in general. Thus, we get interesting results for different objects.
– As long as we have mentioned Spektr-RG, could you explain whether this observatory provides full sky surveys, and why there are several such surveys?
- Here, I should probably say that Spektr-RG is a bit different from the orbital observatories that I have talked about before, and that these observatories ought to be launched from the atmosphere to take observations in x-ray range. In this respect, Spektr-RG is one more step forward. This observatory was launched to the second Sun-Earth Lagrangian point. It is located approximately 4 times farther from the Earth than the Moon.
How to make picturing this point to oneself easier? Well, just imagine a roundabout with a girl holding a bag on one of the chairs. If the girl stretches her hand the bag will protract under the influence of centrifugal force. So we are as if in this bag extended outside, i.e., it is a point where the centrifugal force of our motion compensates for the gravitation of the Earth and Sun taken together. Both the Earth and Sun are located on the same side for us, which is very convenient from the point of view of thermal control and other technical details of the observatory’s life-support system.
Obtaining of full celestial map by observatory Spektr-RG
Further on, we make circles conventionally facing the Earth. We spin on our axis remaining in permanent contact with the Earth. It is very convenient both for data transfer and from the point of view of the observatories thermal balance.
Making such a circle each time, we scan a celestial strip a bit wider than the Moon is. As long as the Earth is rotating around the Sun we also move round the Sun on this roundabout. Eventually. It appears that the strip that we scan is continuously shifting. By way of accumulating such strips we actually scan the whole sky. It means that we are able to monitor the whole sky within half a year by way of moving from one side of the Solar System to another one.
During the next half, the algorithm of motion repeats, yet in a bit different direction. As minimum, it allows for verifying certain systematic effects. Let us assume that some relative non-alignment of telescope axes may be present, or some other additional effects. From the point of view of research, it allows, as minimum, for studying the variability of objects – i.e., the objects were bright and died out. Or, on the contrary, there were objects that we could not see. Then they flashed and vanished. For instance, the tidal disruption of stars by supermassive black holes is the event that can be effectively traced and found in the data of sky survey by way of comparing what we saw in this point half a year ago with the present state of things and what we will see half a year later. The timescale of this phenomenon is a year or several years, so we are capable of noticing an object to flash and die out. An inactive galaxy became bright and returned to its previous state.
Besides, it is possible to study the processes in the Solar System, because we can scan the Earth immediate environment, when the telescope is located in different parts of the Solar System. It is a very interesting effect. The exploration of distant objects is always performed through the prism of what happens directly in the Earth’s immediate environment, both in heliosphere and more distant areas. The process of comparing one scanned image with another is very useful and opens a lot of opportunities. In general, the addition of scanned images results in accumulation of data. Even if you have a persistent object and have detected a dozen reports from it for the first time, next time you may detect a dozen more reports from it at the average. Naturally, fluctuations happen, yet this kind of accumulation is going on. So, say, comparing the distribution of these photons after 3-4 surveys, you will able to distinguish between, say, a point source with radiation lower than the instrument’s response and such a large object as cluster of galaxies. This is also one of the fundamental missions of an observatory. I mean detecting such sources of long-term x-ray radiation that represent cluster of galaxies.
Additional information:
Hectic life of galaxy clusters. Press Center of the Institute for Space Research of RAS
Telescope SRG/eROSITA Discovered large-scale bubbles of hot gas in Milky Way’s halo. Press Center of the Institute for Space Research of RAS
Traveling along x-ray sky with telescope SRG/eROSITA. Press Center of the Institute for Space Research of RAS
Spektr-RG and (possible) discovery of star collapse in the vicinity of two supermassive black holes. Almost a detective story. Press Center of the Institute for Space Research of RAS
Chronicles of black hole recorded in molecular clouds. Elements
Full interactive celestial map. Project of Spektr-RG
Source of photo on the front page: Rast/123rf.com